コンテンツ
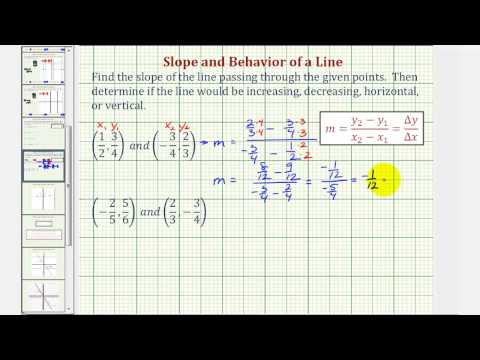
線上の2点を知る、(x1、y1)および(x2、y2)、その比率∆y / ∆x:m =(y2 -y1)/(バツ2 - バツ1)。線がbでy軸と交差し、ポイント(0、b)のいずれかを作成する場合、勾配の定義は、線y = mx + bの勾配切片形式を生成します。直線の方程式がこの形式の場合、直線から直接傾斜を読み取ることができます。これにより、負の逆数なので直線に垂直な直線の傾斜をすぐに決定できます。
TL; DR(長すぎる;読まなかった)
特定の直線に垂直な直線の傾きは、特定の直線の傾きの負の逆数です。与えられた線の勾配がmの場合、垂直線の勾配は-1 / mです。
垂直勾配を決定する手順
定義上、垂直線の勾配は元の線の勾配の負の逆数です。線形方程式を勾配切片形式に変換できる限り、線の勾配を簡単に決定できます。また、垂直線の勾配は負の逆数なので、それも決定できます。
等式の両側にxおよびy項がある方程式があります。それらを方程式の左側で収集し、すべての定数項を右側に残します。方程式は、Ax + By = Cの形式である必要があります。ここで、A、B、Cは定数です。
方程式の形式はAx + By = Cなので、両側からAxを引き、両側をBで除算します。y=-(A / B)x + C / Bが得られます。これは勾配切片形式です。線の勾配は-(A / B)です。
線の勾配は-(A / B)であるため、負の逆数はB / Aです。標準形式の直線の方程式がわかっている場合は、y項の係数をx項の係数で除算するだけで、垂直線の傾きを見つけることができます。
与えられた線に垂直な勾配を持つ無限の数の線があることに留意してください。特定の方程式が必要な場合は、線上の少なくとも1つの点の座標を知る必要があります。
例
1. 3x + 2y = 15y-32で定義される線に垂直な線の傾きはどのくらいですか?
この方程式を標準に変換するには、両側から15yを減算します。3x+(2y-15y)=(15y-15y)-32。減算を実行した後、
3x -13y = -32。
この方程式の形式はAx + By = Cです。垂直線の勾配はB / A = -13/3です。
2. 5x + 7y = 4に垂直で、点(2,4)を通る直線の方程式は何ですか?
方程式を勾配切片形式に変換し始めます:y = mx + b。これを行うには、両側から5xを減算し、両側を7で除算します。
y = -5 / 7x + 4/7。
この線の勾配は-5/7であるため、垂直線の勾配は7/5でなければなりません。
次に、既知の点を使用して、y切片を見つけます。 x = 2のときy = 4なので、
4 = 7/5(2)+ b
4 = 14/5 + bまたは20/5 = 14/5 + b
b =(20-14)/ 5 = 6/5
線の方程式は、y = 7/5 x + 6/5です。両側に5を掛けて簡略化し、右側でxおよびyの項を収集すると、次のようになります。
-7x + 5y = 6