正式には半対数グラフとして知られるロググラフは、1つの軸に線形スケールを使用し、他の軸に対数スケールを使用するグラフです。科学の分野では、変数の1つが他の変数よりもはるかに広い範囲の値を持つ2つの変数のデータポイントをプロットするのに役立ちます。この方法でデータをプロットすることにより、両方の変数が線形にプロットされた場合にはそれほど明白ではないデータの関係を頻繁に観察できます。
対数を定義します。方程式x = b ^ yの場合、yはxの底bへの対数であると言えます。したがって、x = b ^ yの場合、y = logb(x)です。
線形および対数スケールを確立します。リニアスケールのマーキングは個々の単位を示し、1、2、3、4などのラベルが付けられています。対数目盛のマーキングは、対数底のべき乗を示しています。たとえば、10を底とする対数スケールには、10、100、1,000などのラベルが付けられます。
関数を線形グラフにマップします。 xスケールとyスケールの両方が同じ単位を測定します。したがって、図では、緑のy = f(x)は傾き1の直線です。青のY = log10(x)は、x = 1でx軸と交差し、0に近づく正の傾きを持ちます。y=赤の10 ^ xは、y = 1でy軸と交差し、無限大に近づく正の勾配を持ちます。
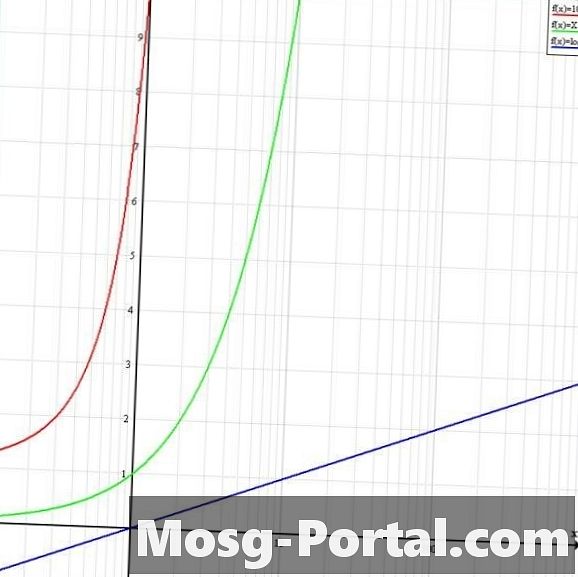
lin-logグラフを使用します。このタイプの対数グラフには、線形スケールのy軸と対数スケールのx軸があります。したがって、x軸のスケールは、y軸に対して10 ^ xの係数で圧縮されます。図では、青色のy = log10(x)は、線形グラフの線y = xに似ています。赤のY = 10 ^ xは、x = 10でy軸と交差し、無限大に近づく正の勾配を持ちます。緑のY = xは、線形グラフではy = 10 ^ xのようになります。
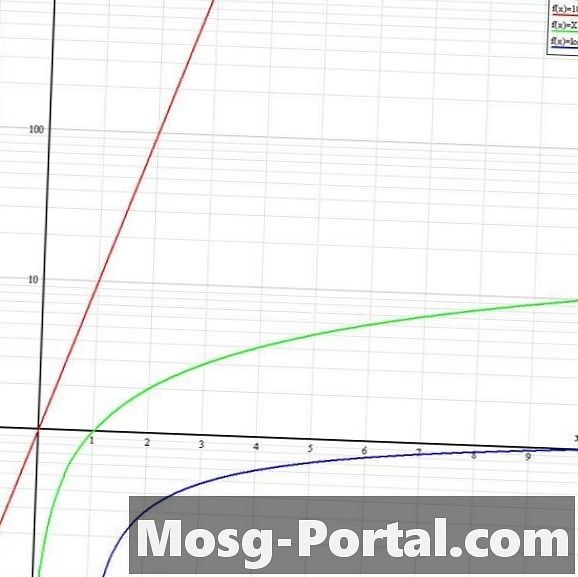
log-linグラフを使用します。このタイプの対数グラフには、対数スケールのy軸と線形スケールのx軸があります。したがって、x軸のスケールは、y軸に対して10 ^ x倍に拡大されます。図では、赤のy = 10 ^ xは線形グラフのy = xのように見えます。緑色のY = xは、線形グラフではy = log10(x)のように見え、y = log10(x)は正の勾配でx軸の下にあり、x軸に漸近的に近づきます。