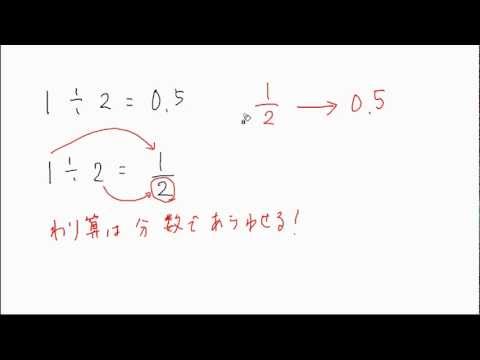
コンテンツ
分数を評価するには、単純化、加算、減算、乗算、除算などの基本的な操作を知っておく必要があります。分数は全体の一部です。 「a / b」と書かれており、「a」は分子、「b」は分母と呼ばれます。これは、全体を「b」個の部分(パイの「b」スライスなど)に分割し、それらの「a」があることを意味します。この概念を念頭に置くと、分数の評価を学ぶのに役立ちます。
分数を減らして小数に変換する
分子と分母の両方を均等に分割する最大数を見つけます。この数が最大公約数です。分数の値を変更せずに、分子と分母をできるだけ小さくする必要があります。これにより、端数が最低の用語に削減されます。
分子と分母の両方を最大公約数で除算します。これは、分数の値を変更しません。たとえば、分数が2/8の場合、分子と分母を2で除算して1/4を取得します。これは2/8に相当しますが、最低の用語に削減されます。分子と分母の両方を5で割って1/3にすることにより、5/15を最低の項に減らします。
分子を分母で除算し、小数の小数形式を取得します。たとえば、2/4は0.25に変換され、1/3は0.33になります。
加減
同じ分母を持つ分数の分子を追加します。合計は同じ分母を取ります。たとえば、2/8 + 3/8 = 5/8です。
分母が同じでない場合は、マルチステッププロセスに従います。同じ分母を持つように分数を操作します。次に、必要に応じて加算または減算します。たとえば、2/6と1/8を追加することを検討してください。
両方の分数を最低の条件に減らします。この例を使用すると、2/6 + 1/8 = 1/3 + 1/8です。
どちらかの分数の分母で均等に除算される最小数を探します。これは最小公倍数です。 3 x 8 = 24および8 x 3 = 24であるため、24は8と3の最小公倍数です。
分数を展開して、分母が同じになるようにします。これは最小公倍数です。 1/3を8/8で乗算して8/24を取得します。 1/8を3/3で乗算して3/24を取得します。
必要に応じて加算または減算します:1/8 + 2/6 = 1/8 + 1/3 = 3/24 + 8/24 = 11/24。減算についても同じことを行います。たとえば、3/5-2/6 = 3/5-1/3 = 9/15-5/15 = 4/15。
乗算と除算
分子のみを乗算して、分数に整数を乗算します。たとえば、5 x 1/8 = 5/8。
分子と分母を一緒に乗算して、分数を別の分数で乗算します。たとえば、3/8 x 2/5 = 6/40 = 3/20。
除算するときは、除算する分数を最初に反転することを除いて、同じ手順に従います。例:3/8÷2/5 = 3/8 x 5/2 = 15/16。