
コンテンツ
電気回路では、回路要素を直列または並列に配置できます。直列回路では、各要素に1つずつ電流が流れる同じブランチを使用して要素が接続されます。並列回路では、要素には独自の分岐があります。これらの回路では、電流は全体を通して異なる経路をたどることができます。
電流は並列回路で異なる経路を取ることができるため、電流は並列回路全体で一定ではありません。代わりに、互いに並列に接続された分岐の場合、各分岐での電圧または電位降下は一定です。これは、電流が各分岐の抵抗に反比例する量で各分岐に分散するためです。これにより、抵抗が最小の場合に電流が最大になり、逆も同様です。
これらの特性により、並列回路で電荷を2つ以上のパスに流すことができるため、安定した効率的な電力システムを通じて、家庭や電気機器の標準候補になります。部品が損傷または破損した場合、回路の他の部分に電気を流し、異なる建物に均等に電力を分配できます。これらの特性は、図と並列回路の例で実証できます。
並列回路図
ヒント
並列回路の例
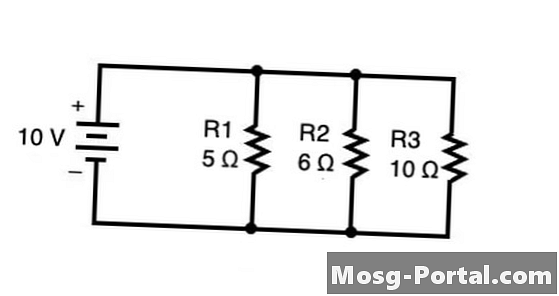
互いに並列に配置された抵抗の合計抵抗を見つけるには、次の式を使用します 1 / R合計 = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn 各抵抗器の抵抗は、式の右側で合計されます。上の図では、オーム(Ω)単位の総抵抗は次のように計算できます。
方程式の両側に1つの項しかない場合は、ステップ3からステップ4に方程式の両側のみを「反転」できることに注意してください(この場合、 1 / R合計 左側に 14/30 Ω 右側に)。
抵抗を計算した後、オームの法則を使用して電流と電圧を計算できます V = I / R その中で V 電圧はボルトで測定され、 私 電流はアンペアで測定され、 R 抵抗はオームです。並列回路では、各パスを流れる電流の合計がソースからの合計電流です。回路内の各抵抗器の電流は、抵抗器の電圧に抵抗を掛けて計算できます。電圧は回路全体で一定であるため、電圧はバッテリーまたは電圧源の電圧です。
並列回路と直列回路
•••Syed Hussain Ather直列回路では、電流は全体にわたって一定であり、電圧降下は各抵抗器の抵抗に依存し、合計抵抗は各抵抗器の合計です。並列回路では、電圧は全体にわたって一定であり、電流は各抵抗器に依存し、総抵抗の逆数は各抵抗器の逆数の合計です。
コンデンサとインダクタを使用して、直列回路と並列回路の電荷を経時的に変化させることができます。直列回路では、合計 キャパシタンス 回路の(変数によって与えられる C)、時間の経過とともに電荷を蓄積するコンデンサの電位は、個々の静電容量の逆数の逆合計であり、 総インダクタンス (私)、時間とともに電荷を放出するインダクタの電力は、各インダクタの合計です。対照的に、並列回路では、総容量は個々のコンデンサの合計であり、総インダクタンスの逆数は個々のインダクタンスの逆数の合計です。
直列回路と並列回路にも異なる機能があります。直列回路では、1つの部品が破損しても、回路に電流がまったく流れません。並列回路では、個々のブランチが開くと、そのブランチの電流のみが停止します。電流には回路を通る複数のパスがあるため、残りのブランチは引き続き機能します。
直列並列回路

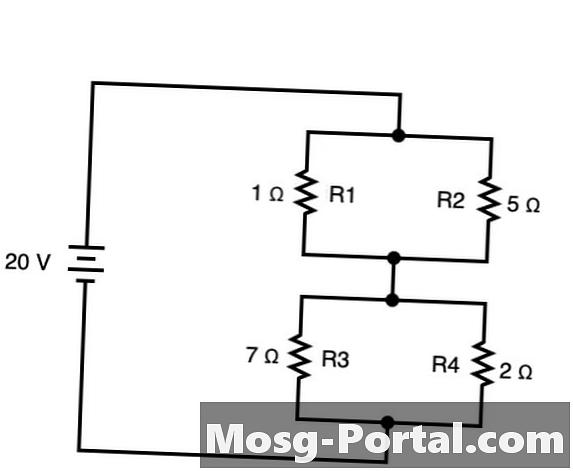
これらの分岐間で電流が一方向に流れるように接続されている両方の分岐要素を持つ回路は、 両方 直列および並列。これらの場合、回路に適した直列および並列の両方からルールを適用できます。上記の例では、 R1 そして R2 互いに平行して形成する R5、そうです R3 そして R4 申込用紙へ R6。これらは、次のように並行して合計できます。
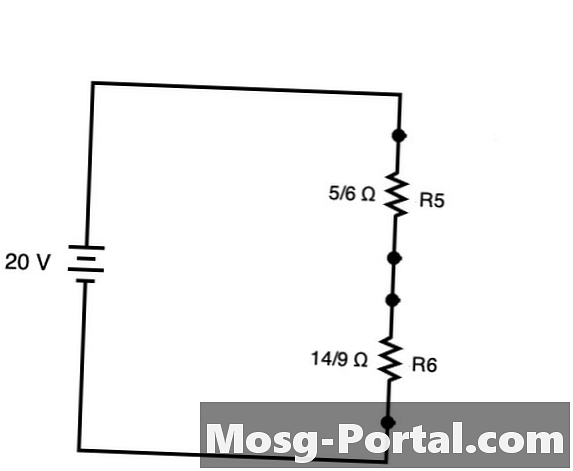
回路を単純化して、上記の回路を作成できます。 R5 そして R6。これらの2つの抵抗は、回路が直列であるかのように簡単に追加できます。
R合計 = 5/6Ω+ 14/9Ω= 45/54Ω+ 84/54Ω= 129/54Ω= 43/18Ωまたは約2.38Ω
で20 V 電圧として、オームの法則は総電流が等しいことを規定します V / R、 または 20V /(43/18Ω)= 360/43 A またはについて 8.37 A. この合計電流で、オームの法則を使用して、R5とR6の両方の電圧降下を決定できます(V = I / R) 同じように。
ために R5, V5 = 360/43 A x 5/6Ω= 1800/258 V またはについて 6.98 V
ために R6, V6 = 360/43 A x 14/9Ω= 1680/129 V またはについて 13.02 V
最後に、これらの電圧降下は R5 そして R6 電流を計算するために元の並列化された回路に戻すことができます R1 そして R2 ために R5 そして R2 そして R3 ために R6 オームの法則を使用。
I1 =(1800/258 V)/ 1Ω= 1800/258 A またはabou_t 6.98 A._
I2 = (1800/258 V) / 5Ω= 1500/43 A またはabou_t 34.88 A._
I3 =(680/129 V) / 7Ω= 4760/129 A またはについて 36.90 A.
I3 =(680/129 V) / 2Ω= 1360/129 A またはについて 10.54 A.