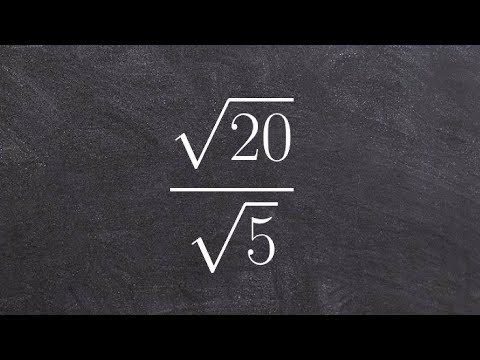
コンテンツ
ラジカル画分は、ポットを飲んだり喫煙したりすることのない、反抗的な画分ではありません。代わりに、ラジカルを含む分数です。通常、最初にコンセプトを導入したときは平方根ですが、後でキューブルート、4番目のルートなども発生する可能性があり、これらもすべてラジカルと呼ばれます。先生があなたに何を求めているかによって、ラジカル分数を単純化する方法は2つあります:ラジカルを完全に因数分解するか、単純化するか、分数を「合理化」します。分子にラジカルがあります。
分数からラジカル式をキャンセルする
あなたの最初のオプションを検討してください、分数からラジカルを因数分解します。これを行うには、実際には2つの方法があります。同じラジカルが存在する場合 すべての用語 分数の上部と下部の両方で、根本的な表現を単純に外してキャンセルすることができます。たとえば、次の場合:
(2√3) / (3√3_)_
分子と分母の各項に存在するため、両方のラジカルを除外できます。それはあなたに残します:
√3/√3 × 2/3
また、分子と分母のゼロ以外の値がまったく同じである分数は1に等しいため、これを次のように書き換えることができます。
1 × 2/3
または単に2/3。
急進的な表現の単純化
前の例の√3のように、簡潔な答えのない急進的な表現に直面することがあります。その場合、通常、根本的な用語をそのまま保持し、ファクタリングやキャンセルなどの基本的な操作を使用して、それを削除または分離します。しかし、時には明らかな答えがあります。次の割合を考慮してください。
(√4)/(√9)
この場合、平方根がわかっていれば、両方の部首が実際によく知られている整数を表していることがわかります。 4の平方根は2、9の平方根は3です。したがって、おなじみの平方根が表示されている場合は、単純な整数形式で分数を書き換えることができます。この場合、次のものがあります。
2/3
これは、キューブルートやその他のラジカルでも機能します。たとえば、8のキューブルートは2で、125のキューブルートは5です。
(3√8) / (3√125)
少し練習すれば、より簡単で簡単に処理できるようになっていることがすぐにわかります。
2/5
分母の合理化
多くの場合、教師は分数の分子に過激な表現を保持させます。しかし、数ゼロのように、ラジカルは分母の分母または底数で現れるときに問題を引き起こします。したがって、ラジカル分数を単純化するように求められる最後の方法は、分数の合理化と呼ばれる操作です。これは、分母からラジカルを取り出すことを意味します。多くの場合、これは、代わりに分子で急進的な式が現れることを意味します。
分数を考慮する
4/_√_5
_√_5を簡単に整数に単純化することはできません。また、それを因数分解しても、次のように、分母にラジカルを持つ分数が残ります。
1/_√_5 × 4/1
したがって、すでに説明した方法はどちらも機能しません。しかし、分数のプロパティを覚えている場合、上と下の両方にゼロ以外の数字がある分数は1になります。
√_5/√_5 = 1
また、他の値を変更せずに他の値を1倍することができるため、実際に分数の値を変更せずに次のように書くこともできます。
√_5/√5 × 4/√_5
一度掛けると、特別なことが起こります。分子は4_√_5になります。これは、分母からラジカルを取り出すことだけが目的だったため、許容範囲です。分子に表示される場合は、対処できます。
一方、分母は √_5 × √5または(√_5)2。そして、平方根と平方は互いに打ち消し合うため、単純に5に単純化されます。したがって、分数は次のようになります。
4_√_5/ 5。分母にラジカルがないため、合理的な分数と見なされます。