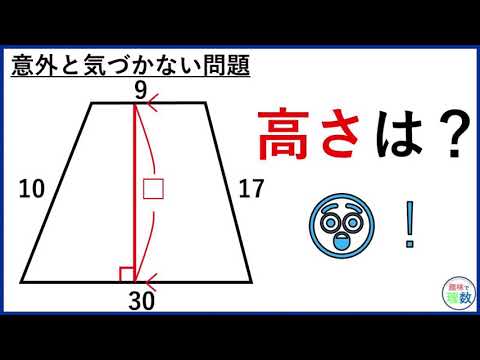
台形の高さは通常、形状の端に沿っていないため、学生は正確な高さを見つけるのが困難です。台形の面積を底と高さに関連付ける幾何学的方程式を学習することで、代数シャッフルをプレイして高さを直接計算できます。
台形の面積の方程式を設定します。 A = h(b1 + b2)/ 2を記述します。ここで、Aは台形の面積を表し、b1はベース長の1つを表し、b2は他のベース長を表し、hは高さを表します。
hを単独で取得するように方程式を並べ替えます。方程式の両側に2を掛けて取得します。 2A = h(b1 + b2)。 2A /(b1 + b2)= hを得るには、方程式の両側を基底の合計で除算します。この方程式は、台形の他の特性に関するhの表現を与えます。
台形の値を高さの方程式に差し込みます。たとえば、基数が4と12で、台形の面積が128である場合、それらを方程式に接続してh = 2 * 128 /(4 + 12)を明らかにします。 1つの数値に単純化すると、高さが16になります。