正方形を取り、2本の対角線を描くと、それらは中央で交差し、4つの直角三角形を形成します。 2つの対角線は90度で交差します。立方体の2つの対角線は、それぞれが立方体の1つのコーナーから反対側のコーナーに向かって走り、中央で交差し、直角に交差すると直感的に推測できます。あなたは間違っているでしょう。立方体の2つの対角線が互いに交差する角度を決定することは、一見すると少し複雑ですが、幾何学と三角法の原理を理解するための素晴らしい練習になります。
エッジの長さを1単位として定義します。定義により、立方体のすべてのエッジの長さは1ユニットと同じです。
ピタゴラスの定理を使用して、1つのコーナーから同じ面の反対側のコーナーまでの対角線の長さを決定します。わかりやすくするために、これを「短い対角線」と呼びます。形成された直角三角形の各辺は1単位なので、対角線は√2に等しくなければなりません。
ピタゴラスの定理を使用して、反対側の面の1つのコーナーから反対側のコーナーまでの対角線の長さを決定します。これを「長い対角線」と呼びます。1辺が1単位に等しく、1辺が「短い対角線」に等しい直角三角形で、√2単位です。斜辺の二乗は辺の二乗の合計に等しいため、斜辺は√3でなければなりません。立方体の1つのコーナーから反対側のコーナーまでの各対角線の長さは√3単位です。
立方体の中心で交差する2つの長い対角線を表す長方形を描きます。それらの交点の角度を見つけたい。この長方形の高さは1ユニット、幅は√2ユニットです。長い対角線は、この長方形の中心で互いに二等分し、2種類の三角形を形成します。これらの三角形の1つは、1辺が1単位に等しく、他の2辺が√3/ 2(長い対角線の長さの半分)に等しい。もう一方にも√3/ 2に等しい2つの辺がありますが、その反対側は√2に等しくなります。三角形の1つだけを分析する必要があるため、最初の三角形を取得して、未知の角度を解きます。
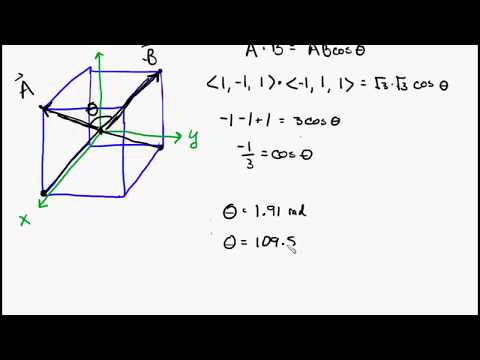
三角形の式c ^ 2 = a ^ 2 + b ^ 2 – 2ab cos Cを使用して、この三角形の未知の角度を解きます。 C = 1、およびaとbの両方が√3/ 2に等しい。これらの値を方程式に代入すると、未知の角度の余弦が1/3であることがわかります。 1/3の逆余弦を取ると、70.5度の角度になります。